<< Click to Display Table of Contents >> Navigation:  Grundlagen > Modul 2: Netzberechnung  > Grundlagen der Netzberechnung > Knoten-Kanten-Modell

Werden mehrere Rohrleitungen zusammengeführt, spricht man von einem Versorgungsnetz. Die Verbindungen der  Rohrleitungen werden als Knoten bezeichnet. Die Rohrleitungen sind die Kanten. Beides zusammen ergibt das sogenannte Knoten-Kanten-Modell (häufig auch als Netzgraph bezeichnet). Zu den Knoten gehören ebenso die Endpunkte der Leitungen. Im folgenden Beispiel ist schematisch ein Netz bestehend aus fünf Leitungen (Ziffern 1 bis 5) und sechs Knoten (a bis f) dargestellt. Die Pfeile der Leitungen definieren eine positive Richtung. Bei der Netzberechnung bedeutet ein positives Vorzeichen für den berechneten Durchfluss, dass die Fließrichtung entlang der angegebenen positiven Pfeilrichtung ist, bei negativem Vorzeichen fließt das Wasser in entgegengesetzte Richtung.  

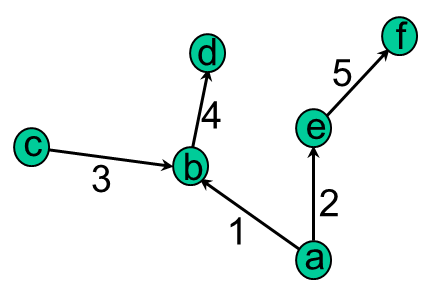
Zur Definition des Netzzusammenhangs wird in der Regel für jedes Rohr der Anfangs- und Endknoten in einer Tabelle angegeben:

 

 

 

Beispiel: Anschlussleitungen aus dem Demo-Modell

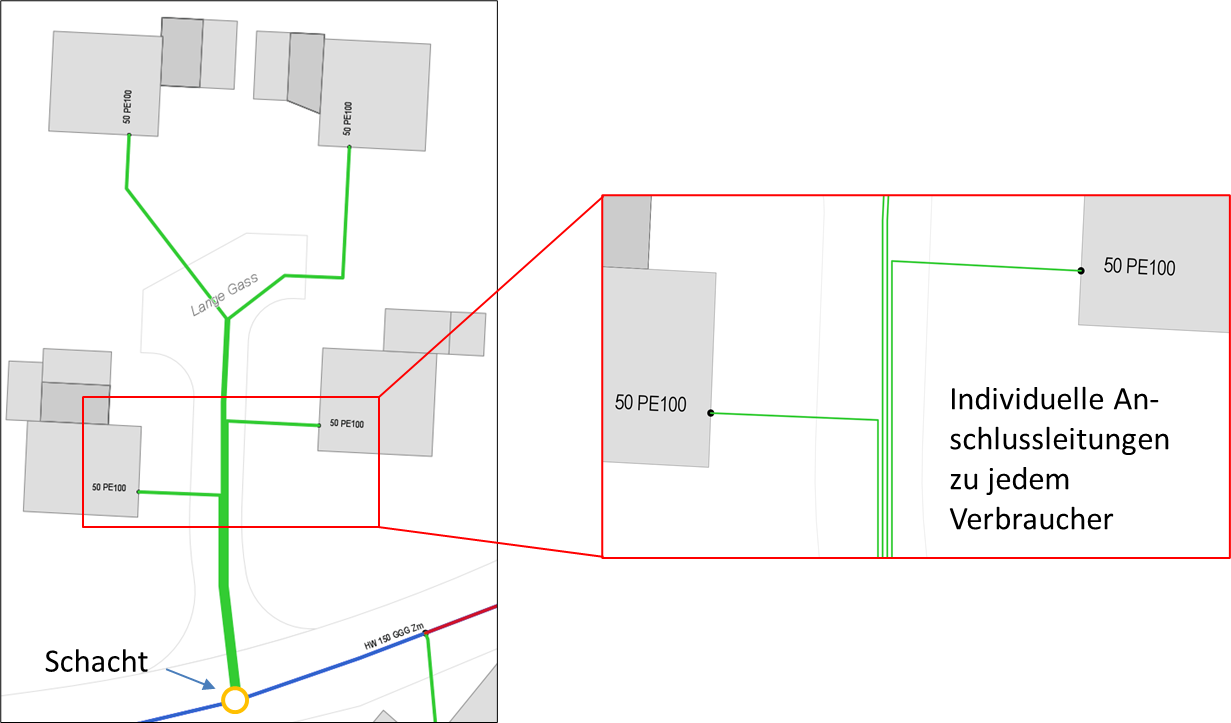
Als Beispiel soll ein Ausschnitt (vier Hausanschlussleitungen aus dem Demo-Modell betrachtet werden. Die GIS-Darstellung des Ausschnitts ist in der folgenden Abbildung zu sehen. Aus einem Schacht, der einer übergeordneten Versorgungsleitung zugeordnet ist, zweigen insgesamt vier Hausanschlussleitungen 50 PE 100 ab, die die vier in ihren Grundrissen dargestellten Gebäude mit Wasser versorgen. Da es sich hier um das sogenannte Württembergische Schachtsystem handelt, ist jedes Gebäude über eine eigene Anschlussleitung mit dem Schacht verbunden. Für die Berechnung wird angenommen, dass der Versorgungsdruck im Schacht bekannt ist. Außerdem sind die geodätischen Höhen und die Jahresverbrauchswerte der Abnehmer sowie die Länge and Materialeigenschaften der Rohre bekannt.

 

 

 

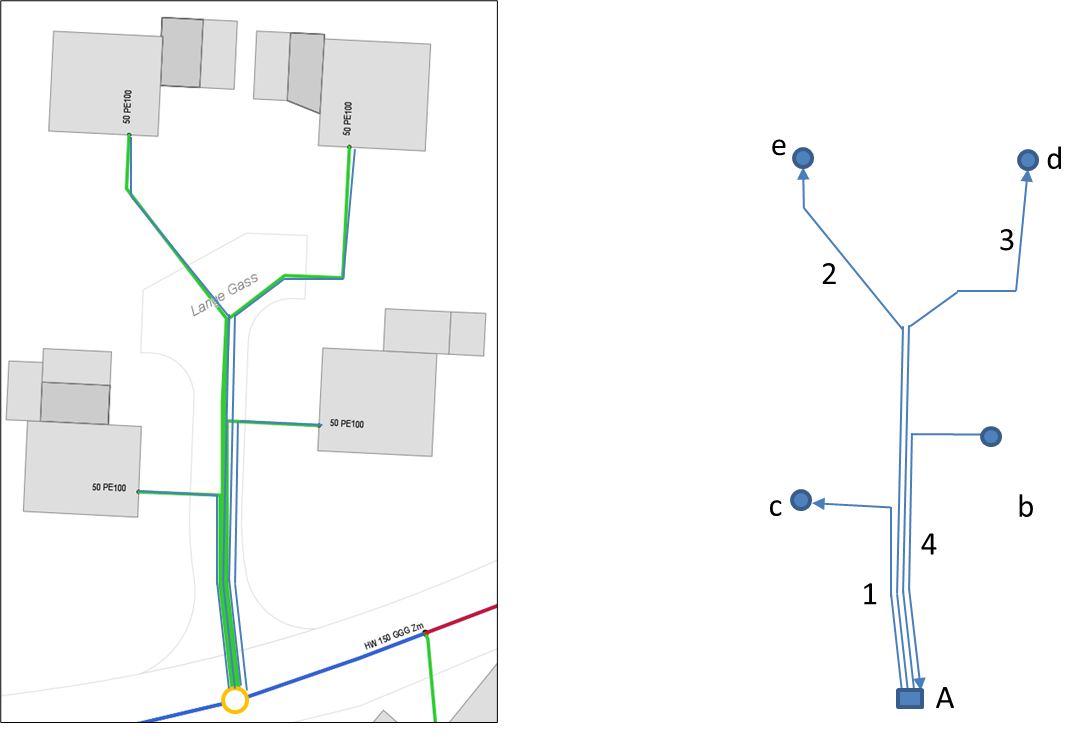
Der erste Schritt zur Netzberechnung besteht in der Abstraktion des GIS-Modells in einem Knoten und Kanten-Modell. In diesem sehr einfachen Beispiel werden Knoten an den Enden der jeweiligen Leitung gesetzt, also am Schacht und an den Hausanschlüssen. Das Modell besteht damit aus fünf Knoten und vier Kanten. Für das Knoten- und Kanten-Modell, welches die logische Verbindung der Objekte zueinander beinhaltet, werden allen Knoten und Rohren eindeutige Bezeichner (Ids: Identifier) zugeordnet. Im Beispiel wurde der Anschlussknoten im Schacht mit "A" und die Anschlussknoten mit den Kleinbuchstaben "b" bis "e" bezeichnet. Für die vier Rohre (Kanten) wurden die Ziffern 1 bis 4 gewählt. Damit lassen sich nun für jede Kante der Anfangs- und Endknoten angeben. Das Knoten-Kantenmodell wird auch als Netzgraph bezeichnet, die Beiziehung zwischen den Kanten und ihren Anfangs- und Endknoten wird Inzidenzbeziehung genannt. Der Netzzusammenhang wird auch als Netztopologie oder Netzgraph (topologisches Modell) bezeichnet. Der Netzgraph ist durch die Angabe von Anfangs- und Endknoten eindeutig definiert.

Die Entscheidung, welcher Knoten als Anfangs- oder Endknoten gewählt wird, ist unbedeutend. Durch die Auswahl wird lediglich eine angenommene positive Fließrichtung (vom Anfangs- zum Endknoten) impliziert. Die tatsächliche Fließrichtung ist in vermaschten Netzen zunächst unbekannt und ergibt sich erst aus der Netzberechnung. folgt die tatsächliche Fließrichtung entgegen der angenommenen wird dies durch ein negatives Vorzeichen für den berechneten Durchfluss (sowie Fließgeschwindigkeit und Druckverlust) ausgedrückt. Im Beispiel wurden zur Veranschaulichung für die Kanten 1 bis 3 eine positive Richtung vom Anschlussknoten zum Verbraucher gewählt, für Kante 4 die umgekehrte Richtung vom Verbraucher zum Anschlussknoten.

Die für die Netzberechnung erforderlichen Daten sind in den folgenden beiden Tabellen zusammengefasst. Die mit "?" gekennzeichneten Einträge sind die bis dahin unbekannten Ergebnisse der Netzberechnung.

Knoten

Rohre

 

Für das vorliegende Beispiel soll nun eine Netzberechnung für einen Spitzenlastfall durchgeführt werden. Das es sich um eine Anschlussleitung handelt, ist nach DVGW 410 der maximale 10s Verbrauch anzusetzen. Der Spitzenlastfaktor f10s wird hier exemplarisch mit 10,0 bezogen auf den Jahresdurchschnittsverbrauch angesetzt. Damit lassen sich nun die für die Berechnung relevanten Entnahmemengen über folgende Formel ermitteln:

.

Für die Abnehmer im Beispiel ergibt sich damit:

,

,

.

Da es sich um ein reines Verästelungsnetz handelt, können die Durchflüsse einfach aus dem Knotengleichgewicht (Massenerhaltung) werden. Dabei sit die positiv definiert Fließrichtung zu beachten. Im speziellen Fall mit dem Württemberger Schachtsystem ist die Berechnung besonders einfach, da jeder Verbraucher direkt über eine unverzweigte Leitung mit dem Schacht verbunden ist und der Durchfluss damit jeweils der Abnahmemenge entspricht:

,  

,  

,  

,  

Beachten Sie das negative Vorzeichen für q4. Die positive Kantenrichtung ist hier von Knoten b nach Knoten A. Die tatsächliche Fließrichtung ist aber natürlich wie bei den anderen Leitungen auch vom Anschlussknoten zum Verbraucher (von A nach b), also entgegengesetzt der Definitionsrichtung.  

Aus den Durchflussmengen lassen sich nun auch die Fließgeschwindigkeiten und Druckverluste berechnen. Die Fließgeschwindigkeiten ergeben sich einfach aus v = q/A, wobei A die Querschnittsfläche des Rohrinneren bezeichnet. Die Reynoldszahl folgt dann aus vD/n (ν: kinematische Viskosität 0,00000131 m2/s):

Rohre

Als letztes sind nun noch die Drücke zu berechnen. Dazu werden zunächst die Druckhöhen bezüglich eines gemeinsamen Druckniveaus (hier Normal Null) durch Abziehen der Druckverluste von der Druckhöhe am Abzweigknoten berechnet. Der manometrische Druck ergibt sich dann nach Abziehen der jeweiligen geodätischen Höhe des Knotens und Multiplikation mit γ:

Knoten

Zur Umrechnung von Druckhöhe in [m] oder [mWs]:

Es gilt: p/γ = H und damit p = γ H = ρ g H

Die Dichte ist abhängig von der Temperatur. Für 10°C gilt: ρ = 1000,3 kg/m3

Mit der Erdbeschleunigung g = 9,81 m/s2 folgt

.

Weiterhin gilt die Umrechnung

.

Die Wichte des Wassers kann damit als Kraft pro Volumen geschrieben werden (an Stelle von Masse pro Volumen bei der Dichte):

Für die Einheit bar gilt die Umrechnung

Die Druckhöhe 1  mWs lässt sich damit folgendermaßen in die Einheit bar umrechnen:

 

Aufgabe: Berechnung des modifizierten Systems (Verästelungsnetz)

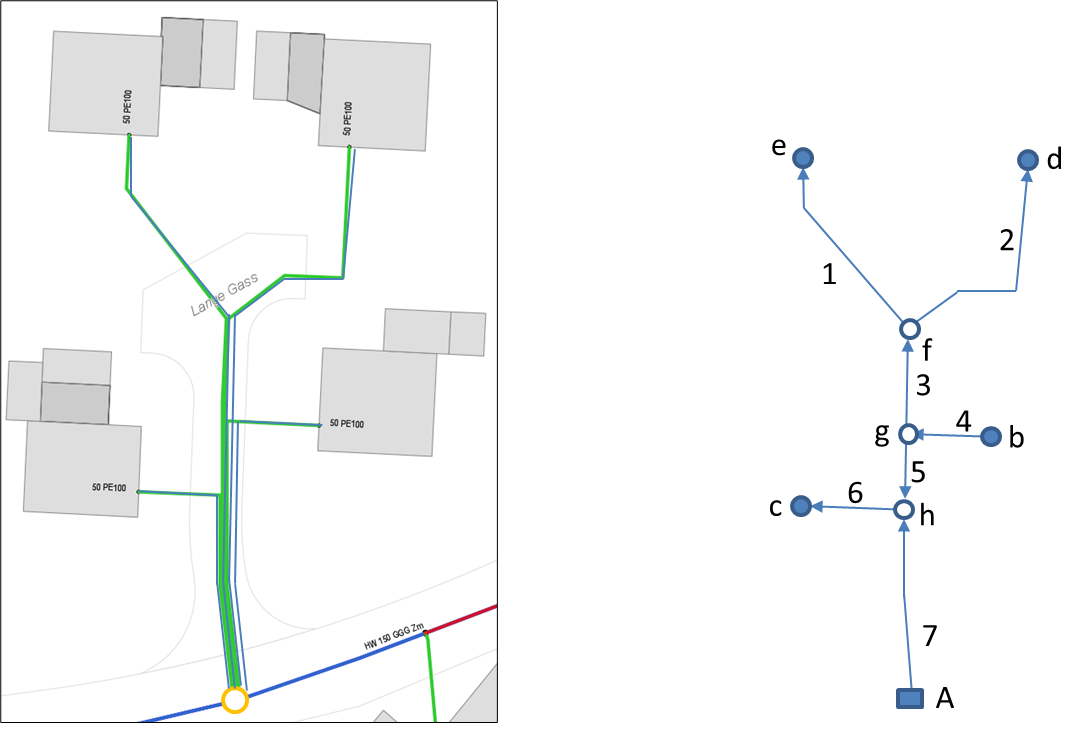
Als nächstes soll nun zur Versorgung der gleichen vier Abnehmer die in obiger Abbildung dargestellte Modifikation des Rohrleitungssystems betrachtet werden. An Stelle der einzelnen parallel verlaufenden Hausanschlussleitungen werden hier alle Abnehmer über eine verzweigte Stichleitung versorgt. Führen Sie nun selbständig eine Netzberechnung durch, indem sie die Tabellen unten vervollständigen.

Hinweis: Die Materialeigenschaften der Rohre sind in den Rohrtabellen im Anhang zu finden

Rohre

 

Knoten